| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
- 차원축소
- 머신러닝
- 코테
- lambda
- OOP
- 데이터 분석
- cpp
- 데이터 마이닝
- 클러스터링
- 파이썬
- numpy 기초
- cpp class
- 기계학습
- 네트워크 기초
- c++
- java
- python
- 합성곱 신경망
- 디자인 패턴
- NumPy
- 코드트리
- 코딩테스트실력진단
- 자바
- 넘파이 기초
- ack
- Design Pattern
- 코딩테스트
- 넘파이
- 넘파이 배열
- Machine Learning
- Today
- Total
준비하는 대학생
[기계학습] k-means 클러스터링 - 최적의 k값 탐색 본문
K-means 알고리즘
K-means 알고리즘은 가장 간단하면서도 널리 사용되는 클러스터링 알고리즘 중 하나입니다. 이 알고리즘은 데이터를 K개의 클러스터로 나누는 방법으로 동작합니다.
K-means 알고리즘의 동작 과정은 다음과 같습니다.
- K개의 클러스터 중심점(centroid)을 임의로 선택합니다.
- 각 데이터 포인트들을 가장 가까운 클러스터 중심점에 할당합니다.
- 할당된 데이터 포인트들의 평균값을 계산하여 새로운 클러스터 중심점을 업데이트합니다.
- 2-3단계를 반복합니다. 클러스터 할당이 변하지 않거나, 미리 정한 반복 횟수에 도달하면 알고리즘이 종료됩니다.
K-means 알고리즘의 단점 중 하나는, 초기 클러스터 중심점의 위치가 무작위로 결정되기 때문에, 다른 결과를 도출할 수 있다는 것입니다. 따라서, 초기 클러스터 중심점의 위치를 바꾸어가며 여러 번 실행하여 결과를 확인하는 것이 필요합니다.
최적의 K값 탐색
K-means 알고리즘을 사용할 때 가장 중요한 문제 중 하나는, 적절한 K값을 선택하는 것입니다. 이번에는 K값을 탐색하는 두 가지 방법인 엘보우 방법과 실루엣 분석에 대해 살펴보겠습니다.
엘보우 방법
엘보우 방법은 K-means 알고리즘을 실행할 때, 클러스터 개수(K)를 점차 증가시키면서 클러스터링을 수행하고, 이에 따른 SSE(Sum of Squared Errors) 값을 계산하여 그래프로 나타내어 최적의 K값을 선택하는 방법입니다.
SSE란 각 데이터 포인트와 해당 클러스터 중심점 사이의 거리를 제곱한 값의 합을 의미합니다. SSE 값이 작을수록 클러스터링의 성능이 좋다고 판단할 수 있습니다. 그래서, 엘보우 방법에서는 클러스터 개수(K)를 증가시키면서 SSE 값을 계산하고, 이를 그래프로 나타냅니다. 이때, SSE 값이 감소하는 정도가 급격하게 줄어드는 지점을 최적의 K값으로 선택합니다. 이 지점은 그래프에서 팔꿈치 모양과 유사하여 "엘보우"라고 부르게 되었습니다.
아래는 엘보우 방법을 사용하여 최적의 K값을 탐색하는 예시 코드입니다.
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
# 엘보우 방법을 사용하여 최적의 K값 탐색
sse = []
for k in range(1, 11):
kmeans = KMeans(n_clusters=k, random_state=0)
kmeans.fit(X)
sse.append(kmeans.inertia_)
# SSE 그래프 그리기
plt.plot(range(1, 11), sse, marker='o')
plt.xlabel('Number of clusters')
plt.ylabel('SSE')
plt.show()위 코드에서 range(1, 11)은 클러스터 개수(K)를 1부터 10까지 변화시키면서 SSE 값을 계산하겠다는 의미입니다. KMeans 함수를 사용하여 K-means 알고리즘을 실행하고, inertia_ 속성을 사용하여 SSE 값을 계산합니다. 계산된 SSE 값을 리스트에 추가하고, 이를 그래프로 나타냅니다.
그래프의 결과는 다음과 같습니다.
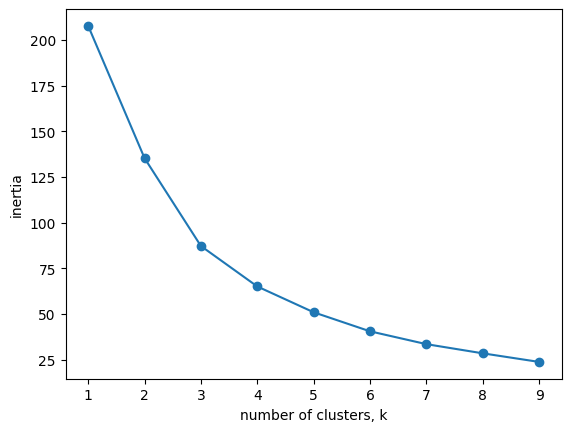
위 그래프에서 팔꿈치 모양을 이루는 지점인 K=3이 최적의 K값이라고 할 수 있습니다.
실루엣 분석 (Silhouette Analysis)
실루엣 분석은 각 데이터 포인트가 속한 클러스터의 일관성을 측정하여 최적의 K값을 찾는 방법입니다. 각 데이터 포인트의 실루엣 계수를 계산하여, 전체 데이터 포인트의 평균 실루엣 계수를 구합니다. 실루엣 계수는 클러스터의 일관성을 나타내며, 값이 높을수록 클러스터링 결과가 좋다는 것을 의미합니다.
실루엣 계수는 다음과 같이 계산됩니다.
- 데이터 포인트 i와 같은 클러스터 내의 모든 데이터 포인트 간의 거리의 평균을 a(i)로 계산합니다.
- 데이터 포인트 i와 가장 가까운 클러스터의 모든 데이터 포인트 간의 거리의 평균을 b(i)로 계산합니다.
- 데이터 포인트 i의 실루엣 계수 s(i)는 (b(i) - a(i)) / max(a(i), b(i))로 계산됩니다.
다음은 실루엣 분석을 사용하여 최적의 K값을 찾는 예시입니다.
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
import matplotlib.pyplot as plt
# 실루엣 분석을 사용하여 최적의 K값 탐색
silhouette_scores = []
for k in range(2, 11):
kmeans = KMeans(n_clusters=k, random_state=0)
kmeans.fit(X)
score = silhouette_score(X, kmeans.labels_)
silhouette_scores.append(score)
# 실루엣 분석 그래프 그리기
plt.plot(range(2, 11), silhouette_scores, marker='o')위 코드에서 range(2, 11)은 클러스터 개수(K)를 2부터 10까지 변화시키면서 실루엣 계수를 계산하겠다는 의미입니다. KMeans 함수를 사용하여 K-means 알고리즘을 실행하고, silhouette_score 함수를 사용하여 실루엣 계수를 계산합니다. 계산된 실루엣 계수를 리스트에 추가하고, 이를 그래프로 나타냅니다.
그래프의 결과는 다음과 같습니다.

위 그래프에서 가장 높은 실루엣 점수를 가지는 K값인 K=2가 최적의 K값이라고 할 수 있습니다.
실루엣 분석은 엘보우 방법과 달리 SSE 값이나 클러스터 개수를 고려하지 않고, 오직 클러스터링의 성능만을 고려합니다. 따라서, 엘보우 방법과 실루엣 분석을 함께 사용하여 최적의 K값을 탐색하는 것이 좋습니다.
결론
K-means 클러스터링에서 최적의 K값을 찾는 것은 매우 중요합니다. 엘보우 방법과 실루엣 분석은 각각 클러스터 내부의 분산과 일관성을 측정하여 최적의 K값을 찾는 방법입니다. 이를 통해 적절한 K값을 찾아 클러스터링 결과를 더욱 정확하게 만들 수 있습니다. 또한, K값을 정하는 것은 사용자의 판단에 따라 다르기 때문에, 여러 가지 방법을 사용하여 최적의 K값을 찾는 것이 좋습니다.
K-means 클러스터링은 데이터를 그룹으로 나누는 데 매우 유용한 방법 중 하나입니다. 하지만, 적절한 K값을 선택하지 않으면 클러스터링 결과가 불안정하거나 부정확할 수 있습니다. 따라서, 엘보우 방법과 실루엣 분석과 같은 방법을 사용하여 최적의 K값을 찾는 것이 중요합니다.
'Programming > Machine learning' 카테고리의 다른 글
| [기계학습] KNN 분석 (분류 및 회귀) (0) | 2023.04.06 |
|---|---|
| [Machine Learning] 주성분 분석(PCA) (0) | 2023.03.28 |
| [기계학습] 군집분석 - 비계층적 클러스터링(k-means) (0) | 2023.03.17 |
| [기계학습] 군집분석 - 계층적 클러스터링 (0) | 2023.03.17 |
| [NumPy] random 난수 생성 (0) | 2023.03.16 |




